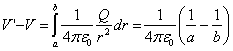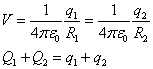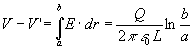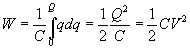QUÉ SON LOS CONDENSADORES?

Se muestra un tutorial de la teoría de condensadores eléctricos y su aplicación en los automóviles.

Uso del condensador electrolítico como acumulador de energía eléctrica

Funcionamiento de un condensador

Será de gran ayuda como complemento a las tutorías en clase, esperando sus comentarios;

Ing. Raúl Matos

POTENCIAL ELECTRICO Y LEY DE GAUSS

Estimados alumnos, en los videos que se muestran se detallan: el potencial eléctrico, diferencia de potencial y la ley de Gauss. Se adiciona unos videos con problemas resueltos.

Problemas Resueltos:

Con la esperanza de ayudarlos mejor en la comprensión del estudio de la Electrostática, he escogido estos videos que son complementarios a las tutorías desarrolladas en la sala virtual.
Espero sus observaciones, dudas y comentarios al respecto, saludos;

Ing. Raúl Matos

Dieléctrico en un Condensador

Efecto del dieléctrico en un condensador

La mayor parte de los condensadores llevan entre sus láminas una sustancia no conductora o dieléctrica. Un condensador típico está formado por láminas metálicas enrolladas, separadas por papel impregnado en cera. El condensador resultante se envuelve en una funda de plástico. Su capacidad es de algunos microfaradios.

La botella de Leyden es el condensador más primitivo, consiste en una hoja metálica pegada en las superficies interior y exterior de una botella de vidrio.

Los condensadores electrolíticos utilizan como dieléctrico una capa delgada de óxido no conductor entre una lámina metálica y una disolución conductora. Los condensadores electrolíticos de dimensiones relativamente pequeñas pueden tener una capacidad de 100 a 1000 mF.

La función de un dieléctrico sólido colocado entre las láminas es triple:

• Resuelve el problema mecánico de mantener dos grandes láminas metálicas a distancia muy pequeña sin contacto alguno.
• Consigue aumentar la diferencia de potencial máxima que el condensador es capaz de resistir sin que salte una chispa entre las placas (ruptura dieléctrica).
• La capacidad de un condensador de dimensiones dadas es varias veces mayor con un dieléctrico que separe sus láminas que si estas estuviesen en el vacío.

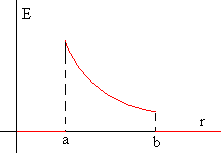
Sea un condensador plano-paralelo cuyas láminas hemos cargado con cargas +Q y –Q, iguales y opuestas. Si entre las placas se ha hecho el vacío y se mide una diferencia de potencial V₀, su capacidad y la energía que acumula serán



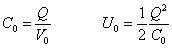
Si introducimos un dieléctrico se observa que la diferencia de potencial disminuye hasta un valor V. La capacidad del condensador con dieléctrico será



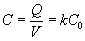
donde k se denomina constante dieléctrica

La energía del condensador con dieléctrico es



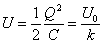
la energía de un condensador con dieléctrico disminuye respecto de la del mismo condensador vacío.

Dieléctrico	Constante dieléctrica
Ámbar	2.7-2.9
Agua	80.08
Aire	1.00059
Alcohol	25.00
Baquelita	4-4.6
Cera de abejas	2.8-2.9
Glicerina	56.2
Helio	1.00007
Mica moscovita	4.8-8
Parafina	2.2-2.3
Plástico vinílico	4.1
Plexiglás	3-3.6
Porcelana electrotécnica	6.5
Seda natural	4-5

Fuente: Manual de física elemental, Koshkin N. I, Shirkévich M. G., Edt. Mir, págs 124-125

Teoría molecular de las cargas inducidas

La disminución de la diferencia de potencial que experimenta el condensador cuando se introduce el dieléctrico puede explicarse cualitativamente del siguiente modo.

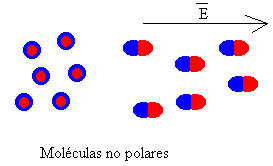
Las moléculas de un dieléctrico pueden clasificarse en polares y no polares. Las moléculas como H₂, N₂, O₂, etc. son no polares. Las moléculas son simétricas y el centro de distribución de las cargas positivas coincide con el de las negativas. Por el contrario, las moléculas N₂O y H₂O no son simétricas y los centros de distribución de carga no coinciden.

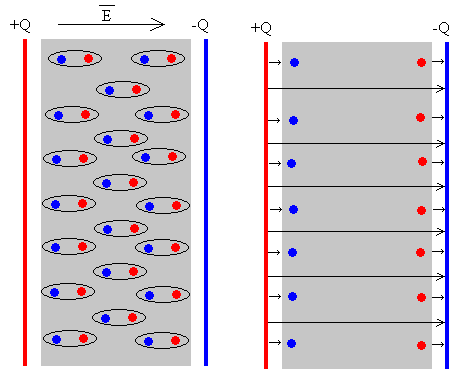
Bajo la influencia de un campo eléctrico, las cargas de una molécula no polar llegan a desplazarse como se indica en la figura, las cargas positivas experimentan una fuerza en el sentido del campo y las negativas en sentido contrario al campo. La separación de equilibrio se establece cuando la fuerza eléctrica se compensa con la fuerza recuperadora (como si un muelle uniese los dos tipos de cargas). Este tipo de dipolos formados a partir de moléculas no polares se denominan dipolos inducidos.

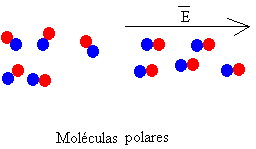
Las moléculas polares o dipolos permanentes de un dieléctrico están orientados al azar cuando no existe campo eléctrico, como se indica en la figura de la derecha. Bajo la acción de un campo eléctrico, se produce cierto grado de orientación. Cuanto más intenso es el campo, tanto mayor es el número de dipolos que se orientan en la dirección del campo.


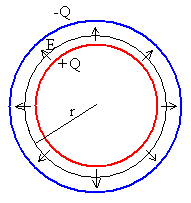
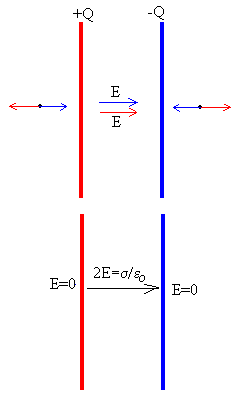
Sean polares o no polares las moléculas de un dieléctrico, el efecto neto de un campo exterior se encuentra representado en la figura inferior. Al lado de la placa positiva del condensador, tenemos carga inducida negativa y al lado de la placa negativa del condensador, tenemos carga inducida positiva.



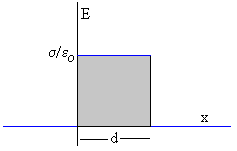
Como vemos en la parte derecha de la figura, debido a la presencia de las cargas inducidas el campo eléctrico entre las placas de un condensador con dieléctrico E es menor que si estuviese vacío E₀. Algunas de las líneas de campo que abandonan la placa positiva penetran en el dieléctrico y llegan a la placa negativa, otras terminan en las cargas inducidas. El campo y la diferencia de potencial disminuyen en proporción inversa a su constante dieléctrica k.=є/є₀

E=E₀/k

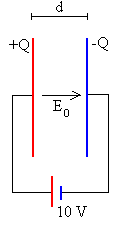
Ejemplo:

Se conecta un condensador plano-paralelo a una batería de 10 V. Los datos del condensador son:

• el área de cada una de sus placas es 0.07 m²,
• la distancia entre las mismas es 0.75 mm.

1. Condensador vacío

          La capacidad del condensador vacío:

La carga Q y densidad de carga σf en las placas del condensador es Q=C0·(V-V’), Q=8.25·10-9 C El campo eléctrico en el espacio comprendido entre las placas del condensador es E0=σf/є0, E0=13333.33 N/C

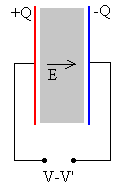
2. Se desconecta el condensador de la batería y se introduce un dieléctrico, por ejemplo, baquelita de k=4.6

          La capacidad del condensador, aumenta

C=k·C₀, C=3.80·10^-9 F

	La diferencia de potencial entre las placas, disminuye V-V’=Q/C, V-V’=2.17 V El campo eléctrico E en el espacio comprendido entre las placas del condensador es E=E0/k, E=2898.6 N/C
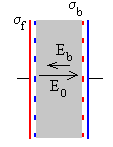	Podemos considerar este campo E, como la diferencia entre le campo E0 producido por las cargas libres existentes en las placas, y el campo Eb producido las cargas inducidas en la superficie del dieléctrico, ambos campos son de signos contrarios. E=E0-Eb

          

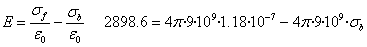
La densidad de carga inducida en el dieléctrico es σ_b=9.23·10^-8 C/m²

Condensadores en paralelo

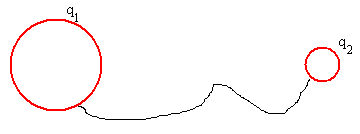
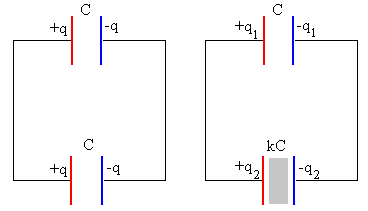
Supongamos que tenemos dos condensadores iguales cargados con la misma carga q, en paralelo. Si introducimos un dieléctrico de constante dieléctrica k en uno de los condensadores. La capacidad del condensador con dieléctrico aumenta, la diferencia de potencial entre sus placas disminuye.

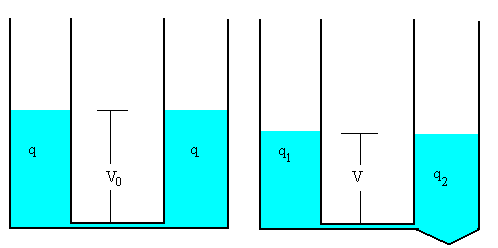
Al unir las placas del mismo signo de los dos condensadores, la carga se repartirá hasta que se igualen de nuevo sus potenciales



La analogía hidráulica se muestra en la figura inferior

2q=q₁+q₂

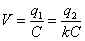
De este sistema de ecuaciones despejamos q₁ y q₂.


Espero estos apuntes les ayuden a comprender mejor el tema de condensadores y dieléctricos.

Saludos;
Ing. Raúl Matos

Condensador Esférico

Capacidad de un condensador esférico

Un condensador esférico está formado por dos superficies conductoras esféricas, concéntricas de radios a y b, cargadas con cargas iguales y opuestas +Q y –Q, respectivamente.

Situamos imaginariamente, una superficie esférica concéntrica de radio r, para determinar el campo eléctrico en las distintas regiones aplicando la ley de Gauss.

Como ya se ha explicado en la página titulada “Modelo atómico de Kelvin_Thomson”, en este problema de simetría esférica, el campo eléctrico tiene dirección radial y su módulo es constante en todos los puntos de una superficie esférica de radio r. El flujo del campo eléctrico E a través de dicha superficie cerrada vale

Determinamos la carga q encerrada en dicha superficie esférica, para distintos valores del radio r, aplicamos la ley de Gauss

• Para r<a, la superficie esférica de radio r, no contiene ninguna carga, q=0, y E=0
• Para a<r<b, la superficie esférica de radio r, contiene una carga, q=+Q,

• Para r>b, la superficie esférica de radio r, contiene una carga, q=+Q-Q=0, y E=0

En la figura, se representa el módulo del campo E en función de r. La diferencia de potencial entre las dos placas es de radios a y b es

La capacidad de un condensador esférico es

Si el radio del segundo conductor esférico es muy grande b→∞, entonces tenemos la capacidad de un condensador esférico de radio R=a

Suponiendo que la Tierra es un conductor esférico de radio R=6370 km, su capacidad sería

Dos esferas conductoras

Sean dos esferas conductoras de radios R₁ y R₂ respectivamente, que están inicialmente aisladas una de la otra y cargadas con cargas Q₁ y Q₂ respectivamente.

Los potenciales de las superficies de las dos esferas son, respectivamente

Se ponen en contacto las dos esferas mediante un cable. La carga pasa de una esfera a la otra hasta que sus potenciales se igualan.

En este sistema de dos ecuaciones con dos incógnitas despejamos q₁ y q₂

El potencial común V vale

Dos esferas conductoras en un campo eléctrico uniforme

Examinamos ahora, el siguiente problema. Dos esferas conductoras del mismo radio R, inicialmente descargadas están unidas mediante un hilo conductor. Se colocan en una región en la que existe un campo eléctrico uniforme E, paralelo al eje X, tal como se muestra en la figura. El centro de la primera esfera está fijada en el origen y el centro de la segunda se desplaza a una distancia x₀.

El radio de las esferas es pequeño para que el efecto de las cargas inducidas en sus superficies sea despreciable.

La diferencia de potencial entre las dos esferas es E·x₀. Pero como están conectadas por un hilo conductor deberán estar al mismo potencial, pasará carga de la primera a la segunda esfera hasta que sus potenciales se igualen. La primera esfera se carga con una carga -q y la segunda con una carga +q.

La diferencia de potencial entre dos esferas de radio R cargadas con cargas +q y –q es

Esta diferencia de potencial debe ser igual a E·x₀

Condensador Cilindrico

Capacidad de un condensador cilíndrico

El campo existente entre las armaduras de un condensador cilíndrico de radio interior a, radio exterior b, y longitud L, cargado con cargas +Q y –Q, respectivamente, se calcula aplicando la ley de Gauss a la región a<r<b, ya que tanto fuera como dentro del condensador el campo eléctrico es cero.

La aplicación del teorema de Gauss, es similar al de una línea cargada,y requiere los siguientes pasos:



1.-A partir de la simetría de la distribución de carga, determinar la dirección del campo eléctrico.

La dirección del campo es radial y perpendicular al eje del cilindro.

2.-Elegir una superficie cerrada apropiada para calcular el flujo

Tomamos como superficie cerrada, un cilindro de radio r, y longitud L. Tal como se muestra en la figura. El cálculo del flujo, tiene dos componentes

• Flujo a través de las bases del cilindro: el campo y el vector superficie son perpendiculares, el flujo es cero.

• Flujo a través de la superficie lateral del cilindro. El campo E es paralelo al vector superficie dS, y el campo es constante en todos los puntos de la superficie lateral, por lo que,

El flujo total es por tanto; E·2p rL

3. Determinar la carga que hay en el interior de la superficie cerrada

La carga en el interior de la superficie cerrada vale +Q, que es la carga de la armadura cilíndrica interior

4.-Aplicar el teorema de Gauss y despejar el módulo del campo eléctrico

Ahora, es fácil demostrar, aplicando el teorema de Gauss que el campo en las regiones r<a y r>b es nulo.

• En el primer caso, si tomamos una superficie cilíndrica de radio r<a y de longitud L, dicha superficie no encierra carga alguna.
• En el segundo caso, si tomamos una superficie cilíndrica de radio r>b y longitud L, la carga total encerrada es +Q-Q=0, es nula, el flujo es cero y el campo es cero.

En la figura, se muestra la representación gráfica del campo E en función de la distancia radial r.

La diferencia de potencial entre las placas del condensador se calcula integrando, (área sombreada de la figura).

La capacidad es



La capacidad solamente depende de la geometría del condensador (radio a y radio b de sus armaduras, y longitud L del condensador)

Si el cilindro interior no está completamente introducido en el exterior, sino solamente una longitud x, la capacidad del condensador será



Energía del condensador

CONDENSADORES ELÉCTRICOS

CONDENSADORES

Se denomina condensador al dispositivo formado por dos conductores cuyas cargas son iguales pero de signo opuesto.

La capacidad C de un condensador se define como el cociente entre la carga Q y la diferencia de potencia V-V’ existente entre ellos.

                     

La  unidad de capacidad es el farad o faradio (F), aunque se suelen emplear submúltiplos de esta unidad como el microfaradio µF=10^-6 F, y el picofaradio, pF=10^-12 F.

Un condensador acumula una energía U en forma de campo eléctrico. La fórmula como demostraremos más abajo es:
                                              
 

Condensador plano-paralelo

En primer lugar, calculamos el campo creado por una placa plana indefinida, cargada con una densidad de carga s , aplicando la ley de Gauss.

Campo creado por una placa plana indefinida, cargada.



Para una placa indefinida cargada, la aplicación del teorema de Gauss requiere los siguientes pasos:

1.-A partir de la simetría de la distribución de carga, determinar la dirección del campo eléctrico.
La dirección del campo es perpendicular a la placa cargada, hacia afuera si la carga es positiva y hacia la placa si la carga es negativa.

2.-Elegir una superficie cerrada apropiada para calcular el flujo
Tomamos como superficie cerrada, un cilindro de base S, cuya generatriz es perpendicular a la placa cargada. El flujo tiene dos contribuciones

• Flujo a través de las bases del cilindro: el campo y el vector superficie son paralelos.

           E·S₁+E·S₂=2EScos0º=2ES

• Flujo a través de la superficie lateral del cilindro. El campo E es perpendicular al vector superficie dS, el flujo es cero.

          El flujo total es por tanto; 2ES

3. Determinar la carga que hay en el interior de la superficie cerrada
La carga (en la figura de color rojo) en el interior de la superficie cerrada vale q=s S, donde s es la carga por unidad de superficie

4.-Aplicar el teorema de Gauss y despejar el módulo del campo eléctrico
                    

El campo producido por una placa infinitamente grande es constante, su dirección es perpendicular a la placa. Esta fórmula la podemos considerar válida para distancias próximas a una placa en comparación con sus dimensiones.


 Campo creado por dos placas planas cargadas con cargas iguales y opuestas.

Supondremos que las placas son infinitamente grandes o bien, que la separación entre las placas es pequeña comparada con sus dimensiones. En la figura de arriba, se muestra el campo producido por cada una de las placas y en la figura de abajo, el campo resultante. Sea un condensador formado por dos placas iguales de área S, separadas una distancia d, pequeña en comparación con las dimensiones de las placas. El campo se cancela en la región del espacio situado fuera de las placas, y se suma en el espacio situado entre las placas. Por tanto, solamente existe campo entre las placas del condensador, siendo despreciable fuera de las mismas.

Como el campo es constante, la  diferencia de potencial entre las placas se calcula multiplicando el módulo del campo por la separación entre las mismas. El área del rectángulo de la figura.

La capacidad del condensador plano-paralelo será



donde Q=s S es la carga total de la placa del condensador.

La capacidad del condensador solamente depende de su geometría, es decir, del área de las placas S y de la separación entre las mismas d.

Energía de un condensador cargado

Para cargar un condensador pasamos carga de la placa de menor a la de mayor potencial y requiere, por tanto, el consumo de energía. Imaginemos que el proceso de carga comienza con ambas placas completamente descargadas y después, sacamos repetidamente cargas positivas de una de ellas y las pasamos a la otra. En un momento dado, tendremos una carga q en las placas y la diferencia de potencial entre las mismas será V tal que

q=C·V
El trabajo necesario para incrementar en dq la carga del condensador será

dW=V·dq
El trabajo total realizado en el proceso de carga, mientras esta aumenta desde cero hasta su valor final Q.