Campo producido por un hilo rectilíneo cargado
En este apartado, vamos a deducir el campo producido en un punto P distante R, de una línea indefinida cargada con una densidad de carga de l C/m.
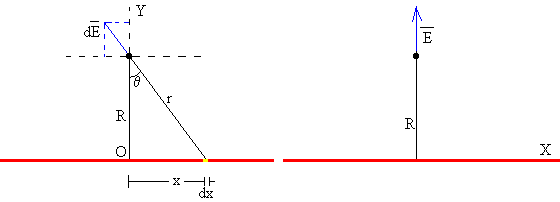
El campo producido por el elemento de carga dq, comprendido entre x y x+dx, tiene la dirección y el sentido indicado en la figura y su módulo es
Este campo tiene dos componentes: una a lo largo del eje vertical Y, y otra a lo largo del eje horizontal X.
La componente horizontal X no es necesario calcularla ya que por simetría se anulan de dos en dos. El elemento de carga dq situado en x, y el elemento de carga dq situado en –x producen campos cuyos módulos son iguales, y cuyas componentes horizontales son iguales y opuestas. El campo total es la suma de las componentes verticales Y
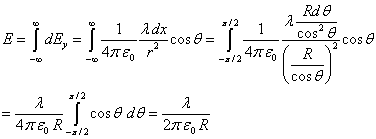
El campo tiene por dirección la perpendicular a la línea indefinida cargada, tal como se indica en la figura de la derecha.
Ley de Gauss
 |
El teorema de Gauss afirma que el flujo del campo eléctrico a
través de una superficie cerrada es igual al cociente entre la carga que hay en
el interior de dicha superficie dividido entre e0.
Para una línea indefinida cargada, la aplicación del teorema de Gauss requiere los siguientes pasos: |
1.-A partir de la simetría de la distribución de carga, determinar la dirección del campo eléctrico.
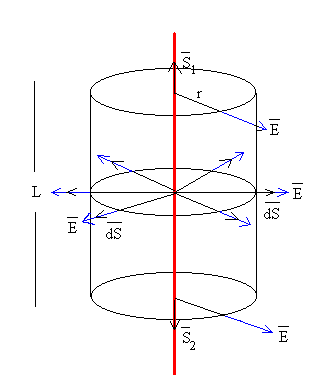
La dirección del campo es radial y perpendicular a la línea cargada
2.-Elegir una superficie cerrada apropiada para calcular el flujo
Tomamos como superficie cerrada, un cilindro de radio r y longitud L.
- Flujo a través de las bases del cilindro: el campo E y el vector superficie S1 o S2 forman 90º, luego el flujo es cero.
- Flujo a través de la superficie lateral del cilindro: el campo E es paralelo al vector superficie dS. El campo eléctrico E es constante en todos los puntos de la superficie lateral,
El flujo total es, E·2p rL
3. Determinar la carga que hay en el interior de la superficie cerrada
La carga que hay en el interior de la superficie cerrada vale q=l L, donde l es la carga por unidad de longitud.
4.-Aplicar el teorema de Gauss y despejar el módulo del campo eléctrico
El mismo resultado que hemos obtenido previamente, pero de una forma mucho más simple.
No hay comentarios:
Publicar un comentario