Condensador Cilindrico

Capacidad de un condensador cilíndrico

El campo existente entre las armaduras de un condensador cilíndrico de radio interior a, radio exterior b, y longitud L, cargado con cargas +Q y –Q, respectivamente, se calcula aplicando la ley de Gauss a la región a<r<b, ya que tanto fuera como dentro del condensador el campo eléctrico es cero.

La aplicación del teorema de Gauss, es similar al de una línea cargada,y requiere los siguientes pasos:



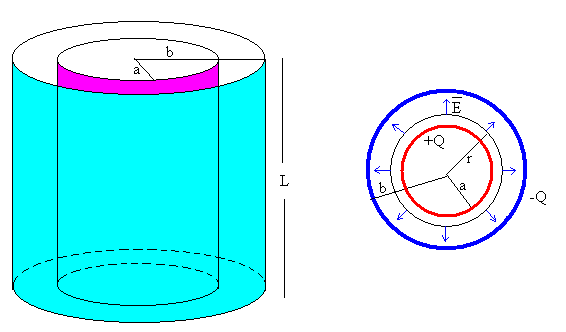
1.-A partir de la simetría de la distribución de carga, determinar la dirección del campo eléctrico.

La dirección del campo es radial y perpendicular al eje del cilindro.

2.-Elegir una superficie cerrada apropiada para calcular el flujo

Tomamos como superficie cerrada, un cilindro de radio r, y longitud L. Tal como se muestra en la figura. El cálculo del flujo, tiene dos componentes

• Flujo a través de las bases del cilindro: el campo y el vector superficie son perpendiculares, el flujo es cero.

• Flujo a través de la superficie lateral del cilindro. El campo E es paralelo al vector superficie dS, y el campo es constante en todos los puntos de la superficie lateral, por lo que,

El flujo total es por tanto; E·2p rL

3. Determinar la carga que hay en el interior de la superficie cerrada

La carga en el interior de la superficie cerrada vale +Q, que es la carga de la armadura cilíndrica interior

4.-Aplicar el teorema de Gauss y despejar el módulo del campo eléctrico

Ahora, es fácil demostrar, aplicando el teorema de Gauss que el campo en las regiones r<a y r>b es nulo.

• En el primer caso, si tomamos una superficie cilíndrica de radio r<a y de longitud L, dicha superficie no encierra carga alguna.
• En el segundo caso, si tomamos una superficie cilíndrica de radio r>b y longitud L, la carga total encerrada es +Q-Q=0, es nula, el flujo es cero y el campo es cero.

En la figura, se muestra la representación gráfica del campo E en función de la distancia radial r.

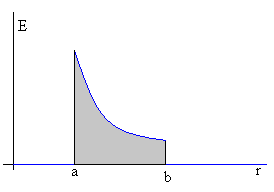La diferencia de potencial entre las placas del condensador se calcula integrando, (área sombreada de la figura).

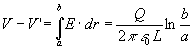La capacidad es



La capacidad solamente depende de la geometría del condensador (radio a y radio b de sus armaduras, y longitud L del condensador)

Si el cilindro interior no está completamente introducido en el exterior, sino solamente una longitud x, la capacidad del condensador será



Energía del condensador