Capacidad de un condensador esférico
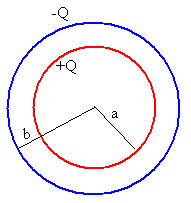 |
Un condensador esférico está formado por dos superficies
conductoras esféricas, concéntricas de radios a y b, cargadas con
cargas iguales y opuestas +Q y –Q, respectivamente.
|
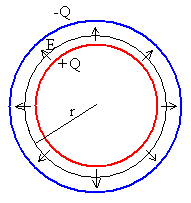
Situamos imaginariamente, una superficie esférica concéntrica
de radio r, para determinar el campo eléctrico en las distintas regiones
aplicando la ley de Gauss.
 |
Como ya se ha explicado en la página titulada “Modelo
atómico de Kelvin_Thomson”, en este problema de simetría esférica, el campo
eléctrico tiene dirección radial y su módulo es constante en todos los puntos de
una superficie esférica de radio r. El flujo del campo eléctrico E
a través de dicha superficie cerrada vale
|
Determinamos la carga q encerrada en dicha superficie
esférica, para distintos valores del radio r, aplicamos la ley de
Gauss
-
Para r<a, la superficie esférica de radio r, no contiene ninguna carga, q=0, y E=0
-
Para a<r<b, la superficie esférica de radio r, contiene una carga, q=+Q,
-
Para r>b, la superficie esférica de radio r, contiene una carga, q=+Q-Q=0, y E=0
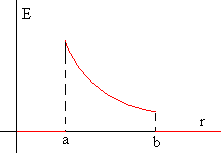 |
En la figura, se representa el módulo del campo E en
función de r.
La diferencia de potencial entre las dos placas es de radios
a y b es
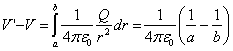 |
La capacidad de un condensador esférico es
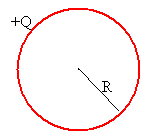 |
Si el radio del segundo conductor esférico es muy grande
b→∞, entonces tenemos la capacidad de un condensador esférico de radio
R=a
|
Suponiendo que la Tierra es un conductor esférico de radio
R=6370 km, su capacidad sería
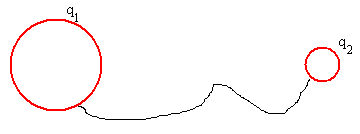
Dos esferas conductoras

Sean dos esferas conductoras de radios R1 y
R2 respectivamente, que están inicialmente aisladas una de la
otra y cargadas con cargas Q1 y Q2
respectivamente.
Los potenciales de las superficies de las dos esferas son,
respectivamente
Se ponen en contacto las dos esferas mediante un cable. La carga pasa de una esfera a la
otra hasta que sus potenciales se igualan.
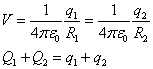
En este sistema de dos ecuaciones con dos incógnitas
despejamos q1 y q2
El potencial común V vale
Dos esferas conductoras en un campo eléctrico uniforme
Examinamos ahora, el siguiente problema. Dos esferas
conductoras del mismo radio R, inicialmente descargadas están unidas
mediante un hilo conductor. Se colocan en una región en la que existe un campo
eléctrico uniforme E, paralelo al eje X, tal como se muestra en la
figura. El centro de la primera esfera está fijada en el origen y el centro de
la segunda se desplaza a una distancia x0.
El radio de las esferas es pequeño para que el efecto de las
cargas inducidas en sus
superficies sea despreciable.
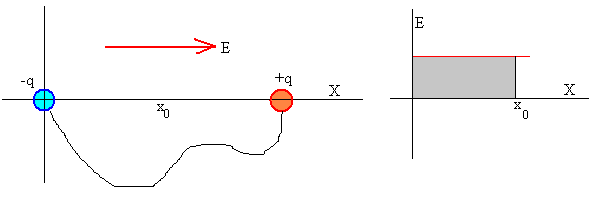
La diferencia de potencial entre las dos esferas es
E·x0. Pero como están conectadas por un hilo conductor deberán
estar al mismo potencial, pasará carga de la primera a la segunda esfera hasta
que sus potenciales se igualen. La primera esfera se carga con una carga
-q y la segunda con una carga +q.
La diferencia de potencial entre dos esferas de radio
R cargadas con cargas +q y –q es
Esta diferencia de potencial debe ser igual a
E·x0
No hay comentarios:
Publicar un comentario