Campo eléctrico y Potencial de una carga puntual
El campo eléctrico de una carga puntual Q en un punto P distante r de la carga viene representado por un vector de:
- módulo
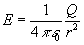
- dirección radial
- sentido hacia afuera si la carga es positiva, y hacia la carga si es negativa
El potencial del punto P debido a la carga Q es un escalar y vale:
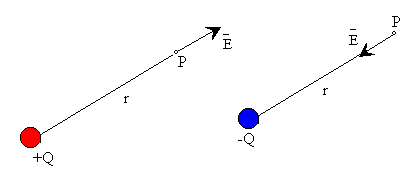
Un campo eléctrico puede representarse por líneas de fuerza, líneas que son tangentes a la dirección del campo en cada uno de sus puntos.
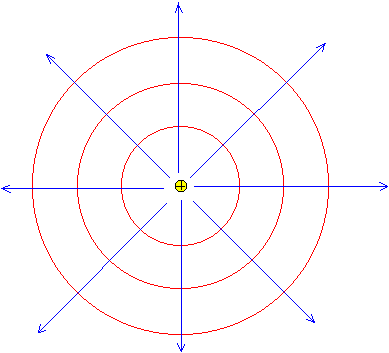
En la figura, se representan las líneas de fuerza de una carga puntual, que son líneas rectas que pasan por la carga. Las equipotenciales son superficies esféricas concéntricas.
Campo eléctrico de un sistema de dos cargas eléctricas
Cuando varias cargas están presentes el campo eléctrico resultante es la suma vectorial de los campos eléctricos producidos por cada una de las cargas. Consideremos el sistema de dos cargas eléctricas de la figura.
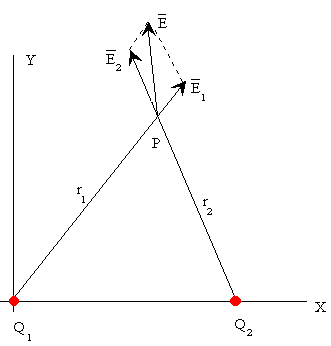 |
El módulo del campo eléctrico producido por cada una de las cargas es Y las componentes del campo total son |
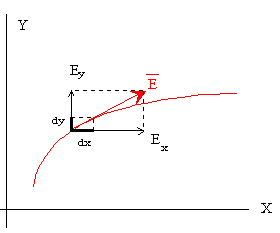 |
Como el campo es tangente a las líneas de fuerza, la ecuación de
las líneas de fuerza es
tal como se muestra en la figura. |
El potencial en el punto P debido a las dos cargas es la suma de los potenciales debidos a cada una de las cargas en dicho punto.
Las superficies equipotenciales cortan perpendicularmente a las líneas de campo. Representaremos en el applet la intersección de las superficies equipotenciales con el plano XY.
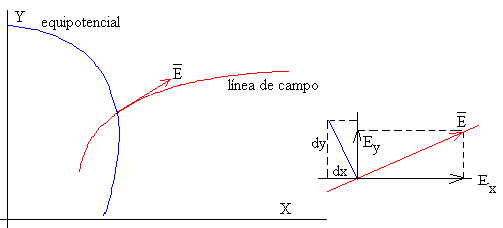
La ecuación de las líneas equipotenciales es
No hay comentarios:
Publicar un comentario