Campo eléctrico en las proximidades de la superficie de un conductor
Dirección del campo eléctrico
La dirección del campo eléctrico en las proximidades del conductor es perpendicular a su superficie como vamos a demostrar, a continuación.
Como el campo eléctrico es conservativo se deberá cumplir que la circulación del campo eléctrico E es cero en un camino cerrado.
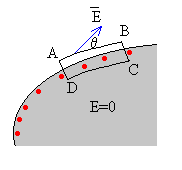 |
Consideremos el camino cerrado ABCD y supongamos que los puntos A y D, están muy próximos entre sí en el interior y en el exterior del conductor, respectivamente. Supongamos que B y C están también muy próximos entre sí. El tramo AB es paralelo a la superficie. |
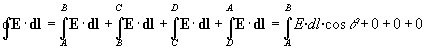
La circulación del campo eléctrico es la suma de cuatro contribuciones, en el tramo CD es nula, por ser el campo en el interior de un conductor cero. Las contribuciones en los lados AD y BC son aproximadamente cero por ser sus longitudes muy pequeñas |AD|=|BC|≈0. La contribución en el lado AB deberá ser por tanto cero para que la suma total sea cero. Esto solamente es posible, si el campo E es perpendicular a la superficie del conductor, es decir, forma 90º con el camino AB.
Por tanto, la consecuencia de que el campo eléctrico sea conservativo, es que la dirección del campo eléctrico en las proximidades de un conductor es perpendicular a la superficie del mismo.
Módulo del campo eléctrico en las proximidades de la superficie de un conductor
El teorema de Gauss nos permite calcular el módulo del campo eléctrico en la superficie de un conductor cuando conocemos la distribución de carga en el mismo.
El teorema de Gauss afirma, que el flujo del campo eléctrico a través de una superficie cerrada es igual al cociente entre la carga en el interior de dicha superficie dividido entre e0.
1.-Determinar la dirección del campo eléctrico.
Como hemos demostrado, la dirección del campo eléctrico en las proximidades del conductor es perpendicular a su superficie.
2.-Elegir una superficie cerrada apropiada para calcular el flujo
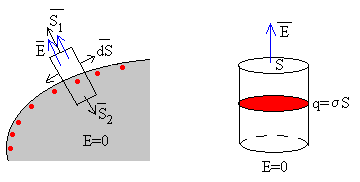
Tomemos como superficie cerrada un cilindro, cuya generatriz es perpendicular a la superficie del conductor. El flujo del campo eléctrico producido por la distribución de carga de s C/m2 en la superficie del conductor consta de tres términos.
- Flujo a través de la superficie lateral. Dado que el campo E es perpendicular al vector dS.
- El flujo del campo eléctrico en la base inferior. Dado que E=0 en el interior del conductor, el flujo a través de esta superficie es cero.
- El flujo a través de la base superior. El campo y el vector superficie son paralelos.
- El flujo total a través de la superficie cilíndrica es:
, Siendo S el área de la base del cilindro.
3. Determinar la carga que hay en el interior de la superficie cerrada
-
La superficie cilíndrica corta la superficie del conductor delimitando un
área S, que contiene una carga q=s S
4.-Aplicar el teorema de Gauss y despejar el módulo del campo eléctrico
Conductor esférico
El conductor más simple de estudiar es un conductor esférico cargado.
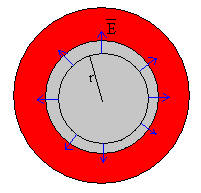
Campo producido por una esfera conductora de radio R cargada con una carga Q.
Para una distribución esférica y unifroem de carga, la aplicación del teorema de Gauss requiere los siguientes pasos:1.-A partir de la simetría de la distribución de carga, determinar la dirección del campo eléctrico.
La distribución de carga tiene simetría esférica luego, la dirección del campo es radial
2.-Elegir una superficie cerrada apropiada para
calcular el flujo
Tomamos como superficie cerrada, una esfera de radio r.
El campo eléctrico E es paralelo al vector superficie dS, y el campo es constante en todos los puntos de la superficie esférica como se ve en la figura, por lo que,
El flujo total es; E·4p r2
3. Determinar la carga que hay en el interior de la superficie cerrada
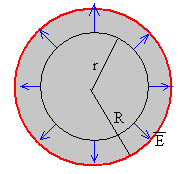 |
Región r<R
Como la carga está en la superficie del conductor, la superficie esférica de radio
r<R no encierra ninguna carga. Luego, E=0.
|
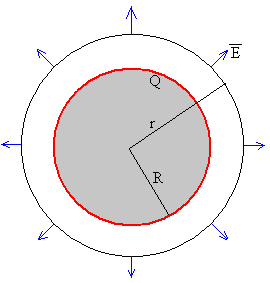 |
Región r>R
La superficie esférica de radio r>R encierra una
carga Q
|
Potencial de la esfera conductora
En la figura se representa el campo eléctrico E en función de r.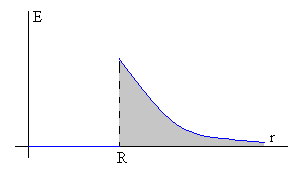
Obtenemos el potencial de la esfera conductora, calculando el
área sombreada en la figura.
Energía de la distribución de cargas
Como la carga Q reside en la superficie esférica y el potencial de dicha carga es V, la energía de la distribución de carga es:Espesor de la capa que contiene el exceso de carga en la superficie de un conductor
Hemos demostrado que un conductor que adquiere una carga
eléctrica, el exceso de carga residirá en la superficie como consecuencia de las repulsiones
entre las cargas individuales. La carga se distribuirá en una capa muy delgada
en la superficie del conductor. La cuestión que se plantea ahora es si la capa
tiene un espesor finito o bien es infinitesimal.
Campo eléctrico producido por una capa esférica uniformemente cargada
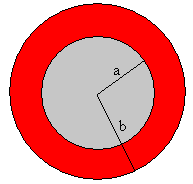 |
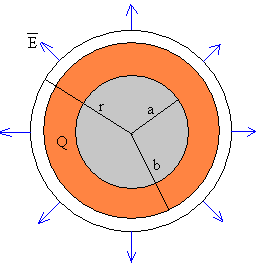
Supongamos que el conductor es esférico, de radio b, y que el exceso de carga reside en una delgada capa comprendida entre a y b uniformemente distribuida en el volumen de dicha capa, tal como se muestra en la figura (el exceso de carga positiva se representa en color rojo). |
El teorema de Gauss afirma que el flujo del campo eléctrico a través de una superficie cerrada es igual al cociente entre la carga en el interior de dicha superficie dividido entre e0.
Para una distribución esférica y uniforme de carga, la aplicación del teorema de Gauss requiere los siguientes pasos:
1.-A partir de la simetría de la distribución de carga, determinar la dirección del campo eléctrico.
La distribución de carga tiene simetría esférica luego, la dirección del campo es radial
2.-Elegir una superficie cerrada apropiada para
calcular el flujo
Tomamos como superficie cerrada, una esfera de radio r.
El campo eléctrico E es paralelo al vector superficie dS, y el campo es constante en todos los puntos de la superficie esférica como se ve en la figura, por lo que,
El flujo total es; E·4p r2
3. Determinar la carga que hay en el interior de la superficie cerrada
- Región a<r<b
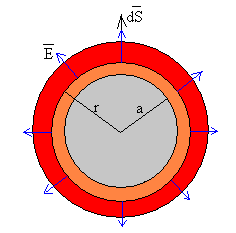 |
Como la carga Q está en el volumen de la capa esférica de
radios a y b, y de volumen (en color rojo)
En la capa esférica comprendida entre a y r hay una carga (en color rosa) |
4.-Aplicar el teorema de Gauss y despejar el módulo del campo eléctrico
La aplicación del teorema de Gauss para las regiones r<a y r>b resulta más simple.
 |
|
 |
La superficie esférica de radio r>b contiene una
carga Q, por lo que el campo vale
|
No hay comentarios:
Publicar un comentario